12月11日 陈旭瑾研究员学术报告

报告人：陈旭瑾 研究员 中国科学院数学与系统科学研究院

报告题目I：Supermodular Maximization under Cardinality and Connectivity Constraints

报告时间：2025年12月11日 15:00-15:50

报告地点：5278论坛 301室

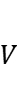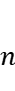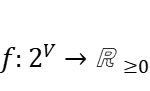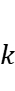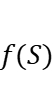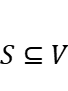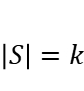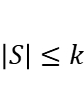摘要：Let be a finite set of elements, be a nonnegative monotone supermodular function, and be a positive integer no greater than . This talk addresses the problem of maximizing over all subsets subject to the cardinality constraint or .  Let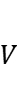be a constant integer. The function 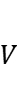is assumed to be 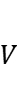-decomposable, meaning there exist 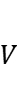(≥ 1) subsets 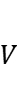of 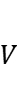, each with a cardinality at most 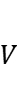, and a corresponding set of nonnegative supermodular functions 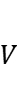, 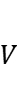such that 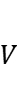holds for all 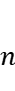. Given 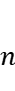as an input, we present a polynomial-time 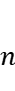-approximation algorithm for this maximization problem, which does not require prior knowledge of the specific decomposition. When the decomposition 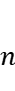is known, an additional connectivity requirement is introduced to the problem. Let 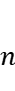be the graph with vertex set 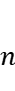and edge set 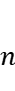. The cardinality constrained solution set 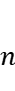is required to induce a connected subgraph in 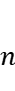. This model generalizes the well-known problem of finding the densest connected 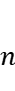-subgraph. We propose a polynomial time 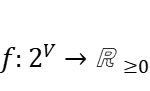-approximation algorithm for this generalization. Notably, this algorithm gives an 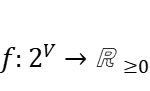-approximation for the densest connected 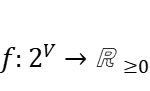-subgraph problem, improving upon the previous best-known approximation ratio of 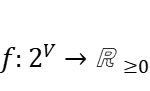. (This is a joint work with Xiaodong Hu, Changjun Wang and Qingjie Ye.)

报告题目II：Packing Feedback Arc Sets in Tournaments Exactly

报告时间：2025年12月11日 16:00-16:50

报告地点：5278论坛 301室

摘要：Let 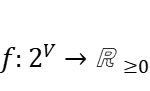be a tournament with a nonnegative integral weight 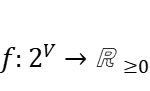on each arc 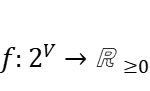. A subset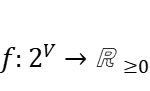of arcs is called a feedback arc set (FAS), if 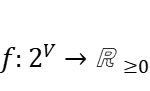contains no cycles (directed). A collection ℱ of FASs (with repetition allowed) is called an FAS packing if each arc 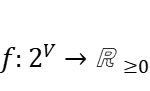is used at most 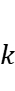times by the members of ℱ. The purpose is to give a characterization of all tournaments 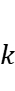with the property that, for every nonnegative integral weight function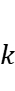defined on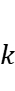, the minimum total weight of a cycle is equal to the maximum size of an FAS packing.

报告人简介：陈旭瑾，中国科学院数学与系统科学研究院研究员，中国运筹学会副理事长。2004年获香港大学博士学位，主要研究兴趣是组合优化的理论和算法，包括算法博弈论、网络优化、多面体组合等。曾获中国青年科技奖、中国运筹学会青年科技奖、国家优秀青年基金。